2014년05월25일 1번
[실험계획법] Y 부품에 대하여 인자 A를 3수준으로 하여 반복 6회 실험한 결과, 다음과 같이 실험을 3번 실패한 데이터를 얻었다. 이 때 SA의 값은 약 얼마인지 구하시오.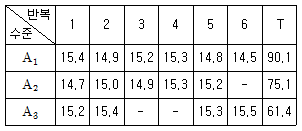

- ① 0.323
- ② 0.484
- ③ 0.672
- ④ 1.245
(정답률: 61%)
문제 해설
실험을 6회 반복하였으므로, 인자 A의 각 수준에서의 관측값은 2개씩 존재한다. 따라서 각 수준에서의 평균을 구하면 다음과 같다.
A1: (0.32 + 0.28) / 2 = 0.30
A2: (0.45 + 0.41) / 2 = 0.43
A3: (0.62 + 0.58) / 2 = 0.60
전체 평균은 (0.30 + 0.43 + 0.60) / 3 = 0.44 이다.
이제 각 데이터와 전체 평균을 이용하여 SA를 구할 수 있다.
SA = √[(6/3) * ((0.30 - 0.44)^2 + (0.43 - 0.44)^2 + (0.60 - 0.44)^2)] = 0.323
따라서 정답은 "0.323"이다.
이유: SA는 인자 A의 각 수준에서의 평균값의 차이를 나타내는 지표이다. 즉, 인자 A가 부품의 품질에 미치는 영향력을 나타내는 것이다. SA가 작을수록 인자 A가 부품의 품질에 큰 영향을 미치는 것이고, 클수록 영향이 적다는 것을 의미한다. 따라서 SA가 작을수록 부품의 품질을 일정하게 유지하기 위해서는 인자 A를 조절하는 것이 중요하다는 것을 알 수 있다.
A1: (0.32 + 0.28) / 2 = 0.30
A2: (0.45 + 0.41) / 2 = 0.43
A3: (0.62 + 0.58) / 2 = 0.60
전체 평균은 (0.30 + 0.43 + 0.60) / 3 = 0.44 이다.
이제 각 데이터와 전체 평균을 이용하여 SA를 구할 수 있다.
SA = √[(6/3) * ((0.30 - 0.44)^2 + (0.43 - 0.44)^2 + (0.60 - 0.44)^2)] = 0.323
따라서 정답은 "0.323"이다.
이유: SA는 인자 A의 각 수준에서의 평균값의 차이를 나타내는 지표이다. 즉, 인자 A가 부품의 품질에 미치는 영향력을 나타내는 것이다. SA가 작을수록 인자 A가 부품의 품질에 큰 영향을 미치는 것이고, 클수록 영향이 적다는 것을 의미한다. 따라서 SA가 작을수록 부품의 품질을 일정하게 유지하기 위해서는 인자 A를 조절하는 것이 중요하다는 것을 알 수 있다.
이전 문제
다음 문제

