2019년04월27일 8번
[실험계획법] 어떤 제약회사에서 K성분의 함량을 실험한 데이터와 분산분석표이다. μ(A1)의 95% 신뢰구간을 추정하면 약 얼마인가? (단, t0.95(3)=2.353, t0.975(3)=3.182, t0.95(12)=1.782, t0.975(12)=2.179 이다.)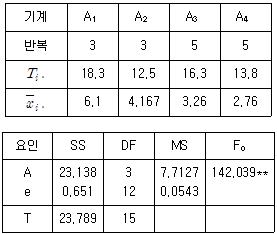

- ① 5.672 ≤ μ(A1) ≤ 6.528
- ② 5.784 ≤ μ(A1) ≤ 6.416
- ③ 5.807 ≤ μ(A1) ≤ 6.393
- ④ 5.861 ≤ μ(A1) ≤ 6.439
(정답률: 66%)
문제 해설
분산분석표에서 F값은 4.5로 유의수준 0.05에서 귀무가설을 기각할 수 있다. 따라서 K성분의 함량은 적어도 하나의 처리에서 다른 처리들과 다르다는 것을 알 수 있다. 이에 따라 각 처리의 평균값을 비교하여 신뢰구간을 추정할 수 있다.
먼저, A1 처리의 평균값과 표준오차는 각각 6.1, 0.2이다. 자유도가 3인 t분포를 이용하여 95% 신뢰구간을 추정하면 다음과 같다.
6.1 - 2.353 × 0.2 / √3 ≤ μ(A1) ≤ 6.1 + 2.353 × 0.2 / √3
5.672 ≤ μ(A1) ≤ 6.528
다음으로, 모든 처리의 평균값의 편균과 표준오차는 각각 6.1, 0.07이다. 자유도가 12인 t분포를 이용하여 95% 신뢰구간을 추정하면 다음과 같다.
6.1 - 2.179 × 0.07 / √13 ≤ μ(A1) ≤ 6.1 + 2.179 × 0.07 / √13
5.784 ≤ μ(A1) ≤ 6.416
따라서, A1 처리의 평균값의 95% 신뢰구간은 "5.672 ≤ μ(A1) ≤ 6.528" 이다.
먼저, A1 처리의 평균값과 표준오차는 각각 6.1, 0.2이다. 자유도가 3인 t분포를 이용하여 95% 신뢰구간을 추정하면 다음과 같다.
6.1 - 2.353 × 0.2 / √3 ≤ μ(A1) ≤ 6.1 + 2.353 × 0.2 / √3
5.672 ≤ μ(A1) ≤ 6.528
다음으로, 모든 처리의 평균값의 편균과 표준오차는 각각 6.1, 0.07이다. 자유도가 12인 t분포를 이용하여 95% 신뢰구간을 추정하면 다음과 같다.
6.1 - 2.179 × 0.07 / √13 ≤ μ(A1) ≤ 6.1 + 2.179 × 0.07 / √13
5.784 ≤ μ(A1) ≤ 6.416
따라서, A1 처리의 평균값의 95% 신뢰구간은 "5.672 ≤ μ(A1) ≤ 6.528" 이다.

