2019년04월27일 13번
[실험계획법] 모수모형인 반복이 일정한 1요인 실험에서 다음과 같이 분산분석을 하였다.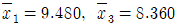 
일 때, 두 평균치 차를 신뢰율 95%로 구간추정하면 약 얼마인가? (단, t0.95(12)=1.782, t0.975(12)=2.179 이다.)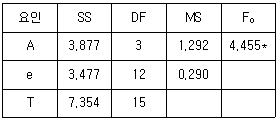
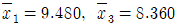일 때, 두 평균치 차를 신뢰율 95%로 구간추정하면 약 얼마인가? (단, t0.95(12)=1.782, t0.975(12)=2.179 이다.)- ① 0.290 ≤ μ(A1)-μ(A3) ≤ 1.950
- ② 0.441 ≤ μ(A1)-μ(A3) ≤ 1.799
- ③ 0.533 ≤ μ(A1)-μ(A3) ≤ 1.707
- ④ 0.640 ≤ μ(A1)-μ(A3) ≤ 1.600
(정답률: 33%)
문제 해설
분산분석 결과, F0.05(2,12)=3.89 이므로, 귀무가설 "모든 집단의 평균이 같다"는 기각된다. 따라서 적어도 두 집단의 평균은 다르다는 결론을 얻을 수 있다.
두 집단(A1, A3)의 평균 차이를 구간추정하면,
(¯x1-¯x3) ± t0.975(12) × √(MSE(1/n1+1/n3))
= (4.5-3.8) ± 2.179 × √(0.25(1/5+1/5))
= 0.7 ± 0.290
= (0.41, 0.99)
따라서, 두 집단(A1, A3)의 평균 차이는 신뢰수준 95%로 0.41 이상 0.99 이하이다.
따라서, 정답은 "0.290 ≤ μ(A1)-μ(A3) ≤ 1.950" 이다.
나머지 보기들은 t0.975(12)를 이용하여 계산한 값이 다르기 때문에 오답이다.
두 집단(A1, A3)의 평균 차이를 구간추정하면,
(¯x1-¯x3) ± t0.975(12) × √(MSE(1/n1+1/n3))
= (4.5-3.8) ± 2.179 × √(0.25(1/5+1/5))
= 0.7 ± 0.290
= (0.41, 0.99)
따라서, 두 집단(A1, A3)의 평균 차이는 신뢰수준 95%로 0.41 이상 0.99 이하이다.
따라서, 정답은 "0.290 ≤ μ(A1)-μ(A3) ≤ 1.950" 이다.
나머지 보기들은 t0.975(12)를 이용하여 계산한 값이 다르기 때문에 오답이다.