2021년05월15일 66번
[기구학 및 CAD] 직교좌표계(x, y, z)에서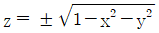 
으로 표현되는 단위 구의 방정식을 매개변수 u, v를 이용 P(u, v) = (cos u cos v, sin u cos v, sin v)의 매개변수식으로 다시 표현하였다면, u, v의 적절한 범위는?
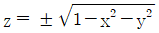으로 표현되는 단위 구의 방정식을 매개변수 u, v를 이용 P(u, v) = (cos u cos v, sin u cos v, sin v)의 매개변수식으로 다시 표현하였다면, u, v의 적절한 범위는?-
①
-
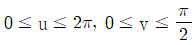
②
-
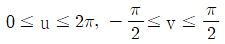
③
-
④
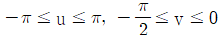
(정답률: 25%)
문제 해설
P(u, v) = (cos u cos v, sin u cos v, sin v)에서 x^2 + y^2 + z^2 = 1을 이용하여 구의 방정식을 표현하면 cos^2 u cos^2 v + sin^2 u cos^2 v + sin^2 v = 1이 된다. 이를 정리하면 cos^2 v = 1 - sin^2 v = 1 - x^2 - y^2이다. 따라서, cos v = sqrt(1 - x^2 - y^2)이고, 이를 P(u, v)에 대입하여 z = sin v = sin(arcsin(sqrt(1 - x^2 - y^2))) = sqrt(1 - x^2 - y^2)가 된다. 따라서, 구의 방정식은 x^2 + y^2 + z^2 = x^2 + y^2 + (1 - x^2 - y^2) = 1이 된다. 따라서, u는 0부터 2π까지, v는 -π/2부터 π/2까지의 범위를 가져야 한다. 따라서, 정답은 ""이다.
"이다.
