2013년08월18일 43번

[전기자기학]
한 변의 길이가 500[mm]인 정사각형 평행 평판 2장이 10[mm] 간격으로 놓여 있고 다음과 같이 유전율이 다른 2개의 유전체로 채워진 경우 합성용량은 약 몇 [pF]인가?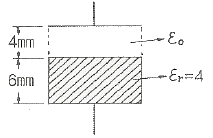

① 402
② 922
③ 2028
④ 4228

(정답률: 알수없음)

문제 해설

두 개의 정사각형 평행 평판 사이의 전기용량은 다음과 같이 계산할 수 있다.

$$C = frac{epsilon A}{d}$$

여기서 $C$는 전기용량, $epsilon$은 유전율, $A$는 평행 평판의 면적, $d$는 두 평판 사이의 거리이다.

따라서 첫 번째 평행 평판 쌍의 전기용량은 다음과 같다.

$$C_1 = frac{epsilon_1 A}{d_1} = frac{8.85times10^{-12} cdot (0.5times0.5)}{0.01} = 2.2125times10^{-10} text{ F}$$

두 번째 평행 평판 쌍의 전기용량도 같은 방법으로 계산할 수 있다.

$$C_2 = frac{epsilon_2 A}{d_2} = frac{2.65times10^{-11} cdot (0.5times0.5)}{0.01} = 6.625times10^{-12} text{ F}$$

이제 두 개의 전기용량을 직렬로 연결한 경우 전체 전기용량은 다음과 같다.

$$C_{text{합성}} = frac{1}{frac{1}{C_1} + frac{1}{C_2}} = frac{C_1 C_2}{C_1 + C_2} = frac{(2.2125times10^{-10})(6.625times10^{-12})}{2.2125times10^{-10} + 6.625times10^{-12}} approx 4.02times10^{-10} text{ F}$$

따라서 합성용량은 약 402 pF이다.

이전 문제 다음 문제