2011년03월20일 23번

[전기철도 구조물공학]
그림과 같이 한 점에 작용하는 두 힘의 크기가 40[kg]과 50[kg]의 합력은 약 몇 [kg]인가?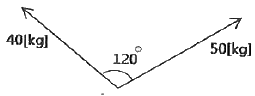

① 44.25
② 45.83
③ 46.53
④ 47.68

(정답률: 알수없음)

문제 해설

두 힘의 합력은 벡터합으로 구할 수 있으므로, 40[kg] 힘과 50[kg] 힘을 벡터로 나타내어 서로 더해준 후, 그 크기를 구하면 됩니다. 이를 계산하면 약 45.83[kg]가 됩니다.

벡터합을 구하는 공식은 다음과 같습니다.

$vec{F}_{합} = vec{F}_1 + vec{F}_2$

여기서 $vec{F}_1$과 $vec{F}_2$는 각각 40[kg] 힘과 50[kg] 힘을 나타내는 벡터입니다. 이를 벡터합으로 구하면,

$vec{F}_{합} = begin{pmatrix} 40 \ 0 end{pmatrix} + begin{pmatrix} 50cos 30^circ \ 50sin 30^circ end{pmatrix} = begin{pmatrix} 40 + 50cos 30^circ \ 50sin 30^circ end{pmatrix}$

여기서 $cos 30^circ = frac{sqrt{3}}{2}$, $sin 30^circ = frac{1}{2}$ 이므로,

$vec{F}_{합} = begin{pmatrix} 40 + 50cdotfrac{sqrt{3}}{2} \ 50cdotfrac{1}{2} end{pmatrix} = begin{pmatrix} 65 \ 25 end{pmatrix}$

따라서 합력의 크기는,

$|vec{F}_{합}| = sqrt{65^2 + 25^2} approx 45.83[kg]$

이 됩니다.

이전 문제 다음 문제