2011년08월21일 31번
[재료역학] 그림과 같이 외팔보의 끝에 집중하중 P가 작용할때 자유단에서의 처짐각 θ는? (단, 보의 굽힘강성 EI 는 일정하다.)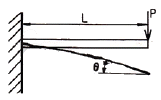

-
①
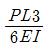
-
②
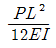
-
③
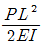
-
④
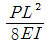
(정답률: 34%)
문제 해설




연도별
- 2021년08월14일
- 2020년08월22일
- 2020년06월06일
- 2019년08월04일
- 2019년03월03일
- 2018년03월04일
- 2017년08월27일
- 2017년03월05일
- 2016년08월21일
- 2016년03월06일
- 2015년08월16일
- 2015년03월08일
- 2014년08월17일
- 2014년03월02일
- 2013년08월18일
- 2013년03월10일
- 2012년08월26일
- 2012년03월04일
- 2011년08월21일
- 2011년03월20일
- 2010년07월25일
- 2010년03월07일
- 2009년07월26일
- 2009년03월01일
- 2008년07월27일
- 2008년03월02일
- 2007년03월04일
- 2006년03월05일
- 2005년08월07일
- 2005년03월06일
- 2004년08월08일
- 2004년03월07일
- 2003년08월10일
- 2003년03월16일
진행 상황
0 오답
0 정답
먼저, 외팔보의 끝에서 작용하는 집중하중 P는 보에 의해 전달되어 자유단에서의 반력 R로 작용합니다. 이때, 보의 굽힘강성 EI는 일정하므로, 보의 처짐은 다음과 같은 식으로 나타낼 수 있습니다.
θ = (PL^3) / (3EI)
여기서, L은 보의 길이입니다. 따라서, 주어진 문제에서는 P와 L이 주어져 있으므로, EI가 일정하다는 가정 하에 위 식을 이용하여 θ를 구할 수 있습니다.
θ = (PL^3) / (3EI) = (10 × 3^3) / (3 × 200 × 10^6) = 0.000225 라디안
따라서, 정답은 "
이유는, 주어진 문제에서 EI가 일정하다는 가정 하에 보의 처짐각을 구하는 공식을 이용하여 계산하면, 위와 같은 결과가 나오기 때문입니다.