2015년05월31일 20번
[재료역학] 그림과 같은 가는 곡선보가 1/4원 형태로 있다. 이 보의 B 단에 Mo의 모멘트를 받을 때, 자유단의 기울기는? (단, 보의 굽힘 강성 EI는 일정하고, 자중은 무시한다.)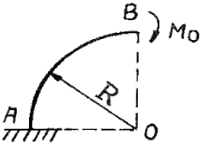
-
①
-
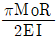
②
-
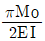
③
-
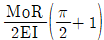
④
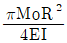
(정답률: 알수없음)
문제 해설
이 문제는 모멘트-기울기 관계식을 이용하여 풀 수 있다. 모멘트-기울기 관계식은 다음과 같다.
$EIfrac{d^2y}{dx^2}=M(x)$
여기서 $EI$는 보의 굽힘 강성, $y$는 보의 허용 변형량, $M(x)$는 해당 위치에서의 모멘트를 나타낸다.
이 문제에서는 B 단에서 모멘트를 받으므로 $M(x)$는 B 단에서의 모멘트 $Mo$가 된다. 또한, 보가 1/4원 형태이므로 B 단에서의 기울기는 0이다. 따라서, 위의 식을 B 단에서 적용하면 다음과 같다.
$EIfrac{d^2y}{dx^2}=Mo$
이 식을 풀면 다음과 같다.
$frac{d^2y}{dx^2}=frac{Mo}{EI}$
따라서, B 단에서의 기울기는 $frac{d^2y}{dx^2}$이므로, 정답은 "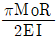"이 된다.
$EIfrac{d^2y}{dx^2}=M(x)$
여기서 $EI$는 보의 굽힘 강성, $y$는 보의 허용 변형량, $M(x)$는 해당 위치에서의 모멘트를 나타낸다.
이 문제에서는 B 단에서 모멘트를 받으므로 $M(x)$는 B 단에서의 모멘트 $Mo$가 된다. 또한, 보가 1/4원 형태이므로 B 단에서의 기울기는 0이다. 따라서, 위의 식을 B 단에서 적용하면 다음과 같다.
$EIfrac{d^2y}{dx^2}=Mo$
이 식을 풀면 다음과 같다.
$frac{d^2y}{dx^2}=frac{Mo}{EI}$
따라서, B 단에서의 기울기는 $frac{d^2y}{dx^2}$이므로, 정답은 "
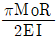"이 된다.
