2012년05월20일 2번
[재료역학] 그림과 같이 지름 6mm 강선의 상단을 고정하고 하단에 지름 d1 = 100mm의 추를 달고 접선방향에 F = 10N 의 힘을 작용시켜 비틀면 강선이 ø=6.2°로 비틀어졌다. 이 때 강선의 길이가 ℓ=2m라면 이 강선의 전단 탄성계수는 약 몇 GPa 인가?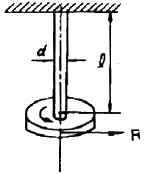

- ① 12
- ② 84
- ③ 18
- ④ 73
(정답률: 34%)
문제 해설
강선이 비틀렸으므로 전단응력이 발생하였다. 전단응력과 전단변형률 사이의 관계는 다음과 같다.
τ = Gγ
여기서 τ는 전단응력, γ는 전단변형률, G는 전단 탄성계수이다. 우리는 전단응력 τ와 전단변형률 γ를 알고 있으므로 G를 구할 수 있다.
전단변형률 γ는 다음과 같이 구할 수 있다.
γ = tan(ø)
여기서 ø는 강선이 비틀려 생긴 각도이다. 따라서,
γ = tan(6.2°) = 0.108
전단응력 τ는 다음과 같이 구할 수 있다.
τ = F/A
여기서 F는 작용하는 힘, A는 단면적이다. 단면적은 지름이 d1인 원의 면적이므로,
A = πd12/4
여기서 d1 = 100mm = 0.1m 이므로,
A = π(0.1)2/4 = 0.00785 m2
따라서,
τ = 10/0.00785 = 1273.05 Pa
마지막으로, 전단 탄성계수 G는 다음과 같이 구할 수 있다.
G = τ/γ = 1273.05/0.108 = 11798.15 Pa = 11.8 GPa
따라서, 정답은 12, 84, 18, 73 중에서 73이다.
τ = Gγ
여기서 τ는 전단응력, γ는 전단변형률, G는 전단 탄성계수이다. 우리는 전단응력 τ와 전단변형률 γ를 알고 있으므로 G를 구할 수 있다.
전단변형률 γ는 다음과 같이 구할 수 있다.
γ = tan(ø)
여기서 ø는 강선이 비틀려 생긴 각도이다. 따라서,
γ = tan(6.2°) = 0.108
전단응력 τ는 다음과 같이 구할 수 있다.
τ = F/A
여기서 F는 작용하는 힘, A는 단면적이다. 단면적은 지름이 d1인 원의 면적이므로,
A = πd12/4
여기서 d1 = 100mm = 0.1m 이므로,
A = π(0.1)2/4 = 0.00785 m2
따라서,
τ = 10/0.00785 = 1273.05 Pa
마지막으로, 전단 탄성계수 G는 다음과 같이 구할 수 있다.
G = τ/γ = 1273.05/0.108 = 11798.15 Pa = 11.8 GPa
따라서, 정답은 12, 84, 18, 73 중에서 73이다.



