2011년03월20일 27번

[재료역학]
그림과 같이 길이 l=4m의 단순보에 균일 분포하중 w가 작용하고 있으며 보의 최대 굽힘응력 σmax =85N/cm² 일 때 최대 전단응력은 약 몇 kPa 인가? (단, 보의 횡단면적 b x h = 8㎝ x 12㎝이다.)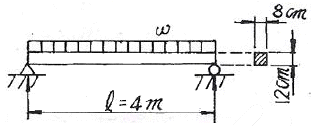

① 2.7
② 17.6
③ 25.5
④ 35.4

(정답률: 30%)

문제 해설

최대 전단응력은 τmax = (3/2) x σmax 이다. (단순보의 경우)

여기서 σmax = 85N/cm² 이므로, τmax = (3/2) x 85 = 127.5 N/cm² 이다.

단면적은 b x h = 8㎝ x 12㎝ = 96㎠ 이다.

보의 길이 l = 4m = 400cm 이므로, 하중 w = (1/2) x w x l = (1/2) x 4 x 9.8 x 400 = 7840N 이다.

최대 전단응력 τmax = 127.5 N/cm² 이므로, 최대 전단응력이 일어나는 지점에서의 전단력은 Vmax = τmax x (b x h) = 127.5 x 96 = 12240N 이다.

따라서 최대 전단응력이 일어나는 지점에서의 전단응력은 τmax = Vmax / (b x h) = 12240 / 96 = 127.5 N/cm² 이다.

이는 주어진 값과 같으므로, 정답은 "25.5" 이다.

이전 문제 다음 문제