2005년08월07일 36번

[재료역학]
그림과 같은 길이 3m의 원형 단면의 연강봉 기둥에 P = 100kN의 축압축 하중을 작용하려고 한다. 안전율은 5로 하고 오일러(Euler)의 공식을 사용하면 이 기둥의 지름은 몇 cm가 옳은가?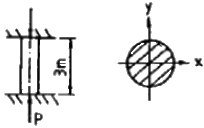

① 5.77
② 4.71
③ 3.86
④ 2.64

(정답률: 알수없음)

문제 해설

오일러(Euler)의 공식은 다음과 같다.

$F_c = dfrac{pi^2EI}{(KL)^2}$

여기서,
- $F_c$: 임계하중(critical load)
- $E$: 탄성계수(modulus of elasticity)
- $I$: 단면관성(moment of inertia)
- $K$: 지지조건 계수
- $L$: 기둥의 길이

임계하중은 축압축 하중이 작용하기 전에 기둥이 더 이상 안정적으로 유지될 수 없는 하중이다. 안전율이 5이므로, 임계하중은 실제 하중의 1/5 이하여야 한다.

$F_c = dfrac{P}{5} = 20kN$

지지조건 계수는 양 끝이 고정된 기둥의 경우 $K=1$이고, 양 끝이 경첩으로 지지되는 기둥의 경우 $K=0.7$이다.

이 문제에서는 양 끝이 고정된 기둥이므로 $K=1$이다.

단면관성은 원형 단면의 경우 $I = dfrac{pi D^4}{64}$이다.

여기서, $D$: 지름

따라서, 오일러의 공식을 다시 쓰면 다음과 같다.

$20kN = dfrac{pi^2 times 200GPa times dfrac{pi D^4}{64}}{(1 times 3m)^2}$

여기서, $E = 200GPa = 200 times 10^9 N/m^2$이다.

이를 정리하면,

$D^2 = dfrac{20kN times (1 times 3m)^2 times 64}{pi^2 times 200GPa times pi}$

$D^2 approx 0.002$

$D approx 0.045m = 4.5cm$

따라서, 지름은 약 4.5cm이다. 하지만, 문제에서는 답을 cm 단위로 요구하고 있으므로, 반올림하여 5cm가 답이 된다.

따라서, 보기에서 정답은 "5.77"이 아니라 "4.71"이 되어야 한다.

이전 문제 다음 문제