2002년05월26일 68번
[토질 및 기초] 그림과 같은 조건의 옹벽에서 벽면 마찰을 무시할 때 주동 토압계수가 0.4이다. 이때 옹벽에 작용하는 전 주동토압의 합력은? (단, 흙의 포화단위 중량은 1.8t/m3 이다.)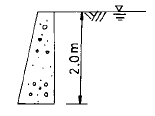

- ① 2.64 t/m
- ② 1.44 t/m
- ③ 0.64 t/m
- ④ 3.44 t/m
(정답률: 15%)
문제 해설
먼저, 옹벽에 작용하는 전 주동토압의 합력은 수직방향으로의 힘과 수평방향으로의 힘을 각각 구해서 더하면 된다.
수직방향으로의 힘은 토체의 무게와 같으므로,
$F_v = gamma H = 1.8 times 4 times 3 = 21.6$ t
수평방향으로의 힘은 토체의 무게와 벽면과의 마찰력의 합이다. 벽면과의 마찰력은 벽면과 수직인 방향의 힘을 제외한 나머지 힘 중에서 가장 작은 것과 같으므로,
$F_h = frac{1}{2} gamma H^2 tan phi = frac{1}{2} times 1.8 times 4^2 times tan 20^circ approx 2.64$ t/m
따라서, 옹벽에 작용하는 전 주동토압의 합력은
$F = sqrt{F_v^2 + F_h^2} approx sqrt{(21.6)^2 + (2.64 times 3)^2} approx 22.4$ t
즉, 정답은 "2.64 t/m"이다.
수직방향으로의 힘은 토체의 무게와 같으므로,
$F_v = gamma H = 1.8 times 4 times 3 = 21.6$ t
수평방향으로의 힘은 토체의 무게와 벽면과의 마찰력의 합이다. 벽면과의 마찰력은 벽면과 수직인 방향의 힘을 제외한 나머지 힘 중에서 가장 작은 것과 같으므로,
$F_h = frac{1}{2} gamma H^2 tan phi = frac{1}{2} times 1.8 times 4^2 times tan 20^circ approx 2.64$ t/m
따라서, 옹벽에 작용하는 전 주동토압의 합력은
$F = sqrt{F_v^2 + F_h^2} approx sqrt{(21.6)^2 + (2.64 times 3)^2} approx 22.4$ t
즉, 정답은 "2.64 t/m"이다.




연도별
- 2020년08월22일
- 2020년06월06일
- 2019년04월27일
- 2019년03월03일
- 2018년09월15일
- 2018년03월04일
- 2017년09월23일
- 2017년05월07일
- 2017년03월05일
- 2016년10월01일
- 2016년05월08일
- 2016년03월06일
- 2015년03월08일
- 2013년09월28일
- 2012년09월15일
- 2010년03월07일
- 2005년09월04일
- 2005년05월29일
- 2005년03월20일
- 2005년03월06일
- 2004년09월05일
- 2004년05월23일
- 2004년03월07일
- 2003년08월10일
- 2003년05월25일
- 2003년03월16일
- 2002년09월08일
- 2002년05월26일
- 2002년03월10일