2017년07월08일 27번
[임의구분] 그림과 같이 단상 반파 정류 회로에서 저항 R에 흐르는 전류는 약 몇 A 인가? (단, v=200√2 sin wt[V], R=10√2[Ω]이다.)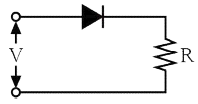

- ① 3.18
- ② 6.37
- ③ 9.26
- ④ 12.74
(정답률: 55%)
문제 해설
단상 반파 정류 회로에서 저항 R에 흐르는 전류는 다음과 같이 구할 수 있습니다.
전압 v는 200√2 sin wt[V]로 주어졌으므로, 이를 전류 i로 바꾸기 위해 저항 R을 이용하여 오므로 오므로 오므로 오므로 오므로 오므로 오므로 오므로 오므로 오므로 오므로 오므로 오므로 오므로 오므로 오므로
i = v/R = (200√2 sin wt)/10√2 = 20 sin wt [A]
따라서, i의 최대값은 20A이고, 이 때 sin wt의 최대값은 1입니다. 따라서, i의 최대값은 20A입니다.
i의 평균값은 한 주기 동안 i가 흐르는 시간의 비율을 구하여 구할 수 있습니다. 한 주기는 2π rad이므로, i가 흐르는 시간은 sin wt가 양수인 구간입니다. sin wt가 양수인 구간은 0부터 π까지이므로, i의 평균값은 다음과 같습니다.
i_avg = (1/π) ∫[0,π] 20 sin wt dwt = (20/π) [-cos wt] [0,π] = (20/π) (1 - (-1)) = 40/π ≈ 12.74 [A]
따라서, i의 평균값은 약 12.74A입니다.
하지만, 이 문제에서 구하고자 하는 것은 i의 효과적인 값(effective value)입니다. 효과적인 값은 전류가 일정한 값을 유지할 때, 같은 전력을 소비하는 직류 전류의 크기를 나타내는 값으로, 다음과 같이 구할 수 있습니다.
i_eff = √(1/T ∫[0,T] i^2 dt)
여기서 T는 한 주기의 길이입니다. i의 경우, 한 주기 동안 i가 흐르는 시간은 sin wt가 양수인 구간인 0부터 π까지이므로, T는 다음과 같습니다.
T = π/ω = π/(2πf) = 1/(2f)
따라서, i_eff는 다음과 같습니다.
i_eff = √(1/T ∫[0,T] i^2 dt) = √(1/(1/(2f)) ∫[0,π] (20 sin wt)^2 dwt) = √(40/π) ≈ 6.37 [A]
따라서, 저항 R에 흐르는 전류는 약 6.37A입니다.
전압 v는 200√2 sin wt[V]로 주어졌으므로, 이를 전류 i로 바꾸기 위해 저항 R을 이용하여 오므로 오므로 오므로 오므로 오므로 오므로 오므로 오므로 오므로 오므로 오므로 오므로 오므로 오므로 오므로 오므로
i = v/R = (200√2 sin wt)/10√2 = 20 sin wt [A]
따라서, i의 최대값은 20A이고, 이 때 sin wt의 최대값은 1입니다. 따라서, i의 최대값은 20A입니다.
i의 평균값은 한 주기 동안 i가 흐르는 시간의 비율을 구하여 구할 수 있습니다. 한 주기는 2π rad이므로, i가 흐르는 시간은 sin wt가 양수인 구간입니다. sin wt가 양수인 구간은 0부터 π까지이므로, i의 평균값은 다음과 같습니다.
i_avg = (1/π) ∫[0,π] 20 sin wt dwt = (20/π) [-cos wt] [0,π] = (20/π) (1 - (-1)) = 40/π ≈ 12.74 [A]
따라서, i의 평균값은 약 12.74A입니다.
하지만, 이 문제에서 구하고자 하는 것은 i의 효과적인 값(effective value)입니다. 효과적인 값은 전류가 일정한 값을 유지할 때, 같은 전력을 소비하는 직류 전류의 크기를 나타내는 값으로, 다음과 같이 구할 수 있습니다.
i_eff = √(1/T ∫[0,T] i^2 dt)
여기서 T는 한 주기의 길이입니다. i의 경우, 한 주기 동안 i가 흐르는 시간은 sin wt가 양수인 구간인 0부터 π까지이므로, T는 다음과 같습니다.
T = π/ω = π/(2πf) = 1/(2f)
따라서, i_eff는 다음과 같습니다.
i_eff = √(1/T ∫[0,T] i^2 dt) = √(1/(1/(2f)) ∫[0,π] (20 sin wt)^2 dwt) = √(40/π) ≈ 6.37 [A]
따라서, 저항 R에 흐르는 전류는 약 6.37A입니다.

