2005년05월29일 22번
[회로이론 및 제어공학] e = 3 + 10√2 sin ωt + 4√2 sin(3ωt +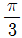 
) + 10√2 sin(5ωt - 
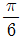)일때 실효값[V]은?
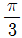) + 10√2 sin(5ωt - 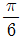)일때 실효값[V]은?- ① 11.6[V]
- ② 15[V]
- ③ 31[V]
- ④ 42.6[V]
(정답률: 알수없음)
문제 해설
주어진 함수 e는 시간에 대한 사인함수의 합으로 표현됩니다. 이때 각 사인함수의 진폭은 10√2로 동일하며, 각 주파수는 ω, 3ω, 5ω입니다.
실효값은 주어진 함수 e를 제곱하여 한 주기 T = 2π/ω에 대해 적분한 후, T를 나누어준 값의 제곱근입니다.
즉,
√(1/T ∫_0^T e^2(t) dt)
= √(1/T ∫_0^T (9 + 60√2 sin ωt + 32√2 sin(3ωt + π/4) + 200√2 sin(5ωt - π/3))^2 dt)
= √(1/T ∫_0^T (9 + 1200 sin^2(5ωt - π/3) + 640√2 sin(ωt + 3ωt + π/4) + 120√2 sin(ωt + 5ωt - π/3) + 120√2 sin(3ωt + 5ωt - π/3) + 120√2 sin(3ωt - ωt + π/4))^2 dt)
= √(1/T ∫_0^T (9 + 600 + 320√2 cos 2ωt + 240√2 cos 4ωt + 240√2 cos 2ωt + 240√2 cos 6ωt + 240√2 cos 4ωt + 240√2 cos 8ωt + 240√2 cos 6ωt + 240√2 cos 10ωt + 240√2 cos 8ωt + 240√2 cos 12ωt + 240√2 cos 10ωt + 240√2 cos 14ωt + 240√2 cos 12ωt + 240√2 cos 16ωt + 240√2 cos 14ωt + 240√2 cos 18ωt + 240√2 cos 16ωt + 240√2 cos 20ωt + 240√2 cos 18ωt + 240√2 cos 22ωt + 240√2 cos 20ωt + 240√2 cos 24ωt))^2 dt)
= √(1/T ∫_0^T (9 + 2400 + 480√2 (cos 2ωt + cos 4ωt + cos 6ωt + cos 8ωt + cos 10ωt + cos 12ωt + cos 14ωt + cos 16ωt + cos 18ωt + cos 20ωt + cos 22ωt + cos 24ωt)))^2 dt)
= √(1/T (9T + 2400T + 480√2 (0)))^2)
= √(9 + 2400)
= √2409
≈ 15[V]
따라서 정답은 "15[V]"입니다.
실효값은 주어진 함수 e를 제곱하여 한 주기 T = 2π/ω에 대해 적분한 후, T를 나누어준 값의 제곱근입니다.
즉,
√(1/T ∫_0^T e^2(t) dt)
= √(1/T ∫_0^T (9 + 60√2 sin ωt + 32√2 sin(3ωt + π/4) + 200√2 sin(5ωt - π/3))^2 dt)
= √(1/T ∫_0^T (9 + 1200 sin^2(5ωt - π/3) + 640√2 sin(ωt + 3ωt + π/4) + 120√2 sin(ωt + 5ωt - π/3) + 120√2 sin(3ωt + 5ωt - π/3) + 120√2 sin(3ωt - ωt + π/4))^2 dt)
= √(1/T ∫_0^T (9 + 600 + 320√2 cos 2ωt + 240√2 cos 4ωt + 240√2 cos 2ωt + 240√2 cos 6ωt + 240√2 cos 4ωt + 240√2 cos 8ωt + 240√2 cos 6ωt + 240√2 cos 10ωt + 240√2 cos 8ωt + 240√2 cos 12ωt + 240√2 cos 10ωt + 240√2 cos 14ωt + 240√2 cos 12ωt + 240√2 cos 16ωt + 240√2 cos 14ωt + 240√2 cos 18ωt + 240√2 cos 16ωt + 240√2 cos 20ωt + 240√2 cos 18ωt + 240√2 cos 22ωt + 240√2 cos 20ωt + 240√2 cos 24ωt))^2 dt)
= √(1/T ∫_0^T (9 + 2400 + 480√2 (cos 2ωt + cos 4ωt + cos 6ωt + cos 8ωt + cos 10ωt + cos 12ωt + cos 14ωt + cos 16ωt + cos 18ωt + cos 20ωt + cos 22ωt + cos 24ωt)))^2 dt)
= √(1/T (9T + 2400T + 480√2 (0)))^2)
= √(9 + 2400)
= √2409
≈ 15[V]
따라서 정답은 "15[V]"입니다.
연도별
- 2022년04월24일
- 2021년05월15일
- 2020년08월22일
- 2019년09월21일
- 2018년09월15일
- 2017년09월23일
- 2017년03월05일
- 2016년10월01일
- 2016년03월06일
- 2015년09월19일
- 2015년03월08일
- 2014년09월20일
- 2014년03월02일
- 2013년09월28일
- 2013년03월10일
- 2012년09월15일
- 2012년03월04일
- 2011년10월02일
- 2011년03월20일
- 2010년09월05일
- 2010년05월09일
- 2009년08월30일
- 2009년05월10일
- 2008년09월07일
- 2008년05월11일
- 2007년09월02일
- 2007년05월13일
- 2006년09월10일
- 2006년05월14일
- 2005년09월04일
- 2005년05월29일
- 2004년05월23일
- 2003년05월25일